1. ASPECTOS TEÓRICOS DEL AISLAMIENTO ACÚSTICO.

    Se incluye este capítulo sobre el aislamiento acústico, desarrollado con cierto detalle, por ser uno de los temas principales para garantizar un confort acústico adecuado. Se aborda desde un punto de vista teórico, haciendo la justa mención a la normativa legal ya que en próximos puntos se tratará ésta con detalle. Dicho tema es una cuestión fundamental a la hora de diseñar un local o recinto para el uso de las personas de cara a una mejora del confort acústico y en el que entra en juego la influencia del exterior sobre el interior. Asimismo, es obvia la necesidad de diseñar de manera especial una sala o local que va a producir un nivel acústico elevado y que pueda ser causa de molestia en estancias colindantes o cercanas.


     1.1. DEFINICIÓN DE AISLAMIENTO. ÍNDICE DE AISLAMIENTO ACÚSTICO, R.

    Podríamos definir, de una manera general, el Aislamiento Acústico entre dos recintos como la cantidad de energía sonora que se pierde o atenúa al propagarse del recinto emisor al recinto receptor. En la práctica se tratará de calcular el aislamiento que produce una partición como puede ser una pared, fachada, forjado etc. (es decir, una superficie o elemento material que separa ambos recintos). Más adelante se explicará la complejidad que supone este problema ya que salvo en condiciones muy concretas, sólo existentes en el laboratorio, cuando se trata de medir el aislamiento que causa una partición es preciso tener en cuenta que el sonido no pasa de un lugar a otro únicamente a través de la partición en cuestión sino que es frecuente que lo haga a través de otros caminos como pueden ser, por ejemplo, los conductos de ventilación, las paredes laterales etc.

    Se define un índice de aislamiento acústico, R, a partir de la relación entre la potencia que se transmite al recinto receptor P_t, y la que incide sobre el elemento de separación del recinto emisor P_i. El coeficiente Tau se denomina coeficiente de transmisión sonora y se define como:

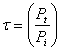
    El Índice de Aislamiento Acústico se define en función de Tau como:


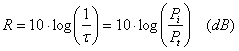
    Esta relación también se conoce como Pérdida de Transmisión y expresa en escala logarítmica qué parte de la energía incidente en una partición que separa dos estancias se transmite o atraviesa dicha separación. Por ejemplo, si tenemos una pared con un índice R=30dB, significa que de la energía sonora que incide en ella tan solo la milésima parte será capaz de atravesarla.


     1.2. ÍNDICES DESCRIPTIVOS DEL AISLAMIENTO ACÚSTICO.

    La manera más sencilla de abordar un problema de aislamiento acústico a ruido aéreo es por medio de la magnitud Aislamiento Bruto, D, que se define como:
    D = L₁ - L₂ (dB)
donde L₁ expresa el nivel de presión sonora en la sala emisora y L₂ el nivel en la sala receptora. De estos niveles es preciso comentar en primer lugar que están promediados tanto en tiempo como en espacio. En segundo lugar decir que los cálculos se han de hacer para cada banda de frecuencia, por ejemplo en tercios de octava.

    El promediado en espacio merece especial atención. Al medir el nivel sonoro en un recinto es necesario hacerlo en diferentes puntos del mismo ya que el campo sonoro no es constante en él. Si se escogen los distintos puntos de manera correcta y se promedian, se tendrá un valor fiable del nivel acústico en dicho recinto. Si obtenemos una sola medida, corremos el riesgo de que sea en un punto donde hay un máximo o un mínimo de campo, lejos del nivel medio en la totalidad del recinto.

    El aislamiento bruto, D, de una partición separadora entre dos salas o estancias, no da una verdadera medida sobre dicha partición ya que la medida del nivel sonoro en la sala receptora en un instante, proviene de la energía sonora de la sala emisora en ese instante más la energía de algún tiempo atrás, que se ha reflejado en las paredes. La reverberación de la habitación receptora está influyendo de esta manera en nuestra medida. Si introducimos un término corrector que contrarreste la influencia de la reverberación, tendremos una medida más precisa y esto se lleva a cabo mediante la magnitud Aislamiento Normalizado, R, que se define:


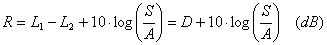
    En esta ecuación, S es la superficie de separación en m² y A es la absorción del local, que podemos calcular despejando en la ecuación de Sabine:


    Por medio de la magnitud R tendremos pues, una medida más precisa que con el aislamiento bruto. Es posible que ambas magnitudes coincidan, (D = R), circunstancia que se dará cuando los valores de S y A sean iguales en m². En otro caso, el valor del aislamiento normalizado será mayor que el del bruto, (D < R).